PREMIER Sample Size Calculation
Sample Size Calculation
In a sample size calculation, the sample size required to demonstrate a previously determined, relevant difference at a defined significance level, with a defined test strength is determined. With the help of the sample size calculation, effects that actually exist should be detected and at the same time guarantee that no effect exists if no statistical difference is measured.
The sample size must not be too small, otherwise no verifiable result regarding a relevant difference is possible after the study has been carried out. In principle, the smaller the expected effect or the greater the variance (standard deviation) of samples, the larger the number of samples required.
The program G*Power, which is available free of charge here , is suitable for calculating the sample size. G*Power is a tool for calculating statistical power analyses for many different t-tests, F-tests, χ2 tests, z-tests and some exact tests. G*Power can also be used to calculate effect sizes and graphically display the results of power analyses. G*Power was developed by General Psychology and Work Psychology of the HHU. (Ref.1)
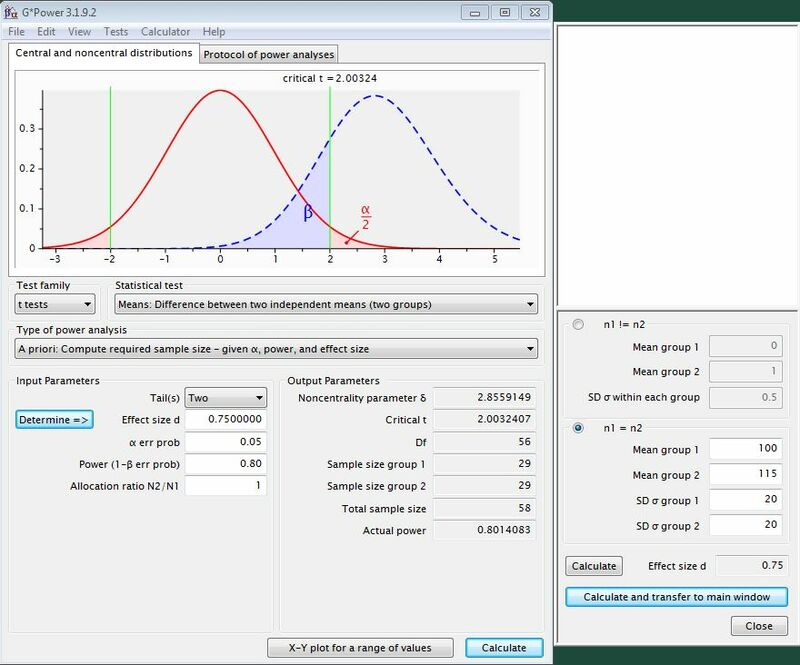
Example
A drug is said to increase the RotaRod test performance of a laboratory animal by 15%. The basic spread of results with the RotaRod is 20%. The same variation is assumed for the drug group. Which number of samples per group is necessary with a significance level of 0.05 and a power of 0.80?
Result
To test this hypothesis in 2 independent animal groups (1 control group, 1 drug group), 29 experimental animals are required in each case.
Pilot Studies
A pilot study can be defined as a small-scale study that helps to test the practicability and feasibility of the methods to be used in a later larger and more comprehensive study. As the conduct of a sufficiently powerful study often requires the involvement of a large number of participants and can therefore be very time consuming and expensive, the conduct of a pilot study on a smaller scale can help to identify unforeseen problems that might affect the quality or the conduct of the study (Ref.1).
Existing methods for calculating sample size typically focus on how to select an appropriate sample size for a pilot study so that various parameters of interest can be estimated with sufficient accuracy (e.g. the effect size, standard deviation of the outcome measure, its reliability, or adherence or wear rates). Such calculations can also play an important role in deciding whether to proceed with the primary study at all. These considerations have led to various guidelines for selecting an appropriate sample size for a pilot study. Further details and references are given in (Ref.2).
References
- Heinrich-Heine-Universität Düsseldorf, Allgemeine Psychologie und Arbeitspsychologie. G*Power: Statistical Power Analyses for Windows and Mac
- Viechtbauer W, Smits L, Kotz D, et al. A simple formula for the calculation of sample size in pilot studies. J Clin Epidemiol. 2015;68(11):1375–1379].